Número F, tiempo de exposición e Irradiancia

Resumen

En esta entrada se describe la relación entre el número F, el tiempo de exposición y la irradiancia percibida por un sensor de imagen.

Abstract
In this entry is described the relationship among f-number, exposure time and irradiance.

Fig. 1 - Cámara fotos Werlisa color

Cuando era niño, mi  padre tenía una cámara de fotos WERLISA color. Recuerdo su lente repleta de ajustes, llena de números incomprensibles y que ninguno de la familia sabía manejar. El único interfaz hombre-máquina era una burda tablilla que teníamos pegada en el interior de su funda de cuero. Allí se indicaban diferentes escenarios de luz (lluvia, sol, nublado, flash) relacionados con la distancia de enfoque, ISO y diafragma, uff, demasiadas variables y muy poca información. Al final las fotos se hacían con la técnica de ensayo y error. ¡Lástima que había que esperar al revelado 6 meses después para conocer el resultado de unos ajustes ya olvidados!

Uno de los grandes misterios para el fotógrafo novel es entender la interrelación entre el número F, longitud focal, tiempo de exposición e ISO.

Todos los conceptos que se expondrán a continuación son aplicables tanto al espectro visible como al infrarrojo usado en cámaras térmicas FLIR, aunque por popularidad, se hará referencia a las cámaras de visible.

Durante esta entrada y para una mejor comprensión de los conceptos expuestos, vamos a dejar la variable ISO fija y estudiar la relación entre el número F y el tiempo de exposición apoyándonos en conceptos físicos de radiometría.

1. DEFINICIONES

Número F (F#): se define como la relación entre la longitud focal de la lente (fl) y el diámetro de la apertura (D). También se la conoce por apertura relativa o f/stop. Se trata de un número adimensional.

$$f\#=\frac{fl}{D}\ \ (1)$$

Por ejemplo, una lente de focal 50 mm con una apertura (diámetro) de 35.7 mm proporciona un F# de 50/35.7= 1.4. Los fotógrafos normalmente hacen referencia a esta lente como aquella que tiene f/stop de f/1.4

Tiempo de exposición Ts [s]: es el tiempo necesario que tenemos que tener expuesto el detector (o película) para formar la imagen. En fotografía se suele medir en fracciones de segundo. Por ejemplo 1/30 s

Ángulo sólido
En geometría plana, un ángulo plano mide la apertura entre dos lineas. La medida del ángulo en radianes, se define entonces como

Fig. 2 - Ángulo plano

$$\delta \theta\left [ rad \right ] =\frac{\delta s}{\delta r}\ \ (2)$$
Donde theta representa el ángulo medido, s la longitud del arco de circunferencia trazado, y r al radio de la circunferencia utilizada para trazar el arco. La medida del ángulo es adimendional.

Si ahora migramos ésta idea a 3 dimensiones e integramos, obtendremos por analogía el concepto de ángulo sólido.

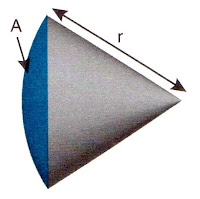Fig. 3 - Ángulo sólido

$$\delta \Omega \left [ sr \right ] =\frac{ \delta A}{ r^{2}}\ \ (3)$$

Radiancia
Una de las unidades básicas de radiometría es la Radiancia (Le). A partir de ella, se derivan otras muchas que iremos viendo. Se define radiancia como la cantidad de flujo [W] radiados dentro de un cono de ángulo sólido [sr] desde una fuente cuyo área se mide en metros cuadrados.

Fig. 4 - Radiancia de una superficie

Para una superficie perpendicular "As" al cono radiado se puede expresar la radiancia como:
$$L_{e}\left [ \frac{W}{m^{2}\cdot sr} \right ]=\frac{\delta \phi }{\delta A_{s}\cdot \delta \Omega }\ \ (4)$$
Para un sistema óptico sin pérdidas, la radiancia permanece invariable a lo largo de todo el camino óptico.

2. FLUJO RECIBIDO POR EL DETECTOR

En la realidad, el flujo radiante de la fuente se atenúa a medida que atraviesa la atmósfera hasta que llega a la lente. Éste flujo resultante que incide sobre la apertura del objetivo, de nuevo se vuelve a atenuar a medida que va atravesando las lentes internas del mismo hasta que se enfoca finalmente sobre el detector. El flujo resultante en función del tiempo de exposición, se convierte en energía y esa energía se transforma en el detector en voltaje que está directamente relacionado con la luminosidad de la imagen.

Fig. 5 - Imagen captada de una fuente radiante

Supongamos ahora una fuente radiante de área As a una distancia R1 de la cámara. El flujo radiante incidente sobre la apertura del objetivo (de área A0) se puede cuantificar como:
$$\phi_{lente}=\iint_{ }^{ }L_{e}\cdot \delta A_{s}\cdot \delta \Omega\ \ (5) $$
Integrando sobre el ángulo sólido abarcado por la apertura de la lente y haciendo simplificaciones por el pequeño ángulo abarcado por el ángulo sólido:
$$\phi_{lente}=L_{e}\frac{A_{o}}{R_{1}^{2}}\cdot A_{s}\cdot T_{atm}\ \ (6) $$
$$R_{1}:distancia\ \ a \ \ la\ \ fuente\\
A_{o}:área\ \ de\ \ apertura\ \ de\ \ la\ \ lente\\
T_{atm}: transmitancia\ \ de\ \ la\ \ atmósfera$$
El flujo radiante que alcanza el plano de la imagen Ai es:
$$\phi_{imagen}=\phi_{lente}\cdot T_{sys}\ \ (7) $$
$$T_{sys}:transmitancia\ \ de\ \ la\ \ lente$$
Expresándolo en los términos anteriores:
$$\phi_{imagen}=L_{e}\frac{A_{o}}{R_{1}^{2}}\cdot A_{s}\cdot T_{atm}\cdot T_{sys}\ \ (8) $$
Si la imagen proyectada Ai es mucho mayor que el área del detector Ad (Ai>>Ad), el flujo incidente sobre el detector se puede expresar como una relación proporcional a las áreas de ambas:
$$\phi_{detector}=\phi_{imagen}\cdot \frac{A_{d}}{A_{i}}\ \ (9) $$
Teniendo en cuenta las ecuaciones  8 y 9:
$$\phi_{detector}=L_{e}\frac{A_{o}}{R_{1}^{2}}\cdot A_{s}\cdot \frac{A_{d}}{A_{i
.}}\cdot T_{atm}\cdot T_{sys}\ \ (10) $$
Por simetría del flujo sobre la lente y usando aproximación paraxial para los ángulos, se puede escribir:
$$\tfrac{A_{s}}{R_{1}^{2}}=\tfrac{A_{i}}{R_{2}^{2}}\ \ (11)$$
es decir
$$A_{s}=A_{i}\frac{R_{1}^{2}}{R_{2}^{2}}\ \ (12)$$
Sustituyendo en la ecuación 10 tenemos:
$$\phi _{detector}=\frac{L_{e}\cdot A_{o}\cdot A_{d}}{R_{2}^{2}}\cdot T_{atm}\cdot T_{sys}\ \ (13)$$
Asumiendo una apertura circular de la lente, el área de la apertura será:
$$A_{o}=\pi \frac{D^{2}}{4}\ \ (14)$$
$$D:diámetro\ \ de\ \ la\ \ lente$$
Por otro lado, R1 y R2 están relacionados con la longitud focal (fl) por la ecuación 15 como se indica en la figura 6:

Fig. 6 - Formación de imagen por aproximación con lente delgada

$$\frac{1}{R_{1}}+\frac{1}{R_{2}}=\frac{1}{fl}\ \ (15)$$
Pero cuando R1 es mucho mayor que R2 (R1>>R2) o tiende a infinito, tenemos:
$$fl=R_{2}\ \ (16)$$
y podemos expresar el número F (F#) de la forma:
$$F\#=\frac{R_{2}}{D}\ \ (17)$$
Sustituyendo las ecuaciones 14, 16 y 17 en 13, el flujo captado por el detector será:
$$\phi _{detector}\left [ W \right ]=\frac{\pi }{4}\frac{L_{e}\cdot A_{d}}{f\#^{2}}\cdot T_{atm}\cdot T_{sys}\ \ (18)$$

3. ENERGÍA RADIANTE SOBRE EL DETECTOR

El flujo captado por el detector multiplicado por el tiempo de exposición de la imagen se convierte en energía que a su vez se transforma en voltaje gracias a la electrónica del propio sensor. Este voltaje estará directamente relacionado con la luminosidad de la imagen.
$$Q_{e}\left [ J \right ]=\frac{\pi }{4}\frac{L_{e}\cdot A_{d}}{f\#^{2}}\cdot T_{s}\cdot T_{atm}\cdot T_{sys}\ \ (19)$$
3.1 ANÁLISIS DE LA ECUACIÓN ENERGÍA RADIANTE SOBRE EL DETECTOR
Según la ecuación 19 para mantener el mismo nivel de luminosidad en la imagen podemos actuar sobre varios factores. Vamos a ver cómo afecta cada uno de los parámetros sin variar los demás.

• Le: cambiar la radiancia al doble (el doble de luz en la escena) supone el doble de energía en el detector. Ésto permitiría por ejemplo disparar con la mitad del tiempo de exposición. Ésta variable muchas veces no es manipulable por el fotógrafo (por ejemplo luz ambiente). Modificar Le supondría añadir focos o el uso de flash en la escena.
• Ad: cuanto mayor sea el tamaño del pixel del sensor de la cámara, mayor energía recibirá. Una cámara digital será más sensible cuanto mayor sea su tamaño de pixel y lo hará de forma proporcional. Ésto nos permitirá fotografiar escenas con poca luz sin necesidad de usar grandes tiempos de exposición o ISO alto. Éste es uno de los motivos del gran tamaño de las cámaras profesionales.
• Ts: cambiar el tiempo de exposición nos permitirá modificar la energía percibida por el detector. Al doble de tiempo de exposición, doble de energía acumulada.
• Tatm: sobre la transmitancia atmosférica poco podemos hacer. Es la atenuación que sufre la energía al atravesar la atmósfera y depende de la distancia y de las condiciones ambientales. La transmitancia siempre será menor o igual que 1 siendo el ideal 1. Dias nublados tendrán mala transmitancia y dias despejados se acercarán al ideal. También, a mayor distancia, menor transmitancia.
• Tsys: es la transmitancia del sistema de lentes que se usa. Sobre ésta variable, el fotógrafo sí puede actuar usando objetivos de calidad. Los buenos objetivos presentarán transmitancias altas.
• f#: desde el punto de vista de energía (sin tener en cuentra otros factores como profundidad de campo), interesa usar numeros f# pequeños. Cuanto más pequeño es f# más luminoso es el objetivo. Además ésta variable actuá al cuadrado y pequeñas variaciones influyen drásticamente en la energía percibida. Teniendo en cuenta la ecuación 17, cuanto más grande sea la apertura de la lente, mejor.

3.2 INFLUENCIA DEL NÚMERO F

De la ecuación 18, para una radiancia Le fija, se puede justificar que la irradiancia recibida por el detector (energía por unidad de superficie del detector), es inversamente proporcional al cuadrado el número F# y directamente proporcional al tiempo de exposición.
$$E_{e}\left [ \frac{W}{m^{2}} \right ]=\propto\frac{T_{s}}{f_{\#}^{2}} \ \ (20)$$
Si se mantiene invariable el tiempo de exposición y sólo modificamos f#, se puede establecer la siguiente tabla de proporcionalidades que se encuentra en muchos libros de óptica.

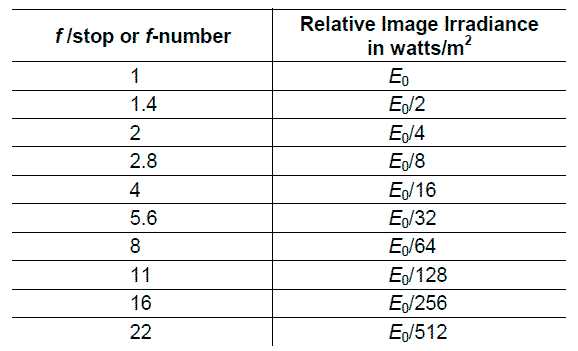Fig. 7 - Irradiancia percibida en función del número F

Por ejemplo, si la irradiancia percibida a F/1 es E0, cuando cambiamos a F/1.4 la irradiancia se reduce a la mitad.

Supongamos la siguiente hipótesis de partida donde la irradiancia es 100% a F/1 con un tiempo de exposición de 1 segundo. Expresado la irradiancia en función del número F y el tiempo de exposición se puede ver en la figura 8 la interrelación entre ambas variables.

Fig. 8 - Irradiancia Ee = f(F#,Ts)

 En la figura 9 se muestran las curvas de irradiancia constante en función del número F y del tiempo de exposición.

Fig. 9 - Curvas de irradiancia constante

3.3 ¿CÓMO AFECTA LA ISO?

Hasta ahora, todo lo expuesto es manteniendo la ISO fija a un determinado valor. veamos su influencia sobre la imagen.

Básicamente, aumentar ISO significa aumentar la ganancia electrónica en la conversión de energía-voltaje. Es decir, con la misma energía percibida por el detector, aumentar la ISO daría la sensación de una percepción de mayor energía (mayor luminosidad en la imagen). Sería el equivalente a desplazar la figura 8 en el eje z (irradiancia) hacia arriba.

De la misma manera, bajar la ISO significaría reducir la ganancia electrónica en la conversión energía-voltaje. Sería el equivalente a desplazar la figura 8 en el eje z (irradiancia) hacia abajo.

REFERENCIAS
[1] - Alexander D. Ryer (1997). The light measurement handbook. ISBN 0-9658356-9-3
[2] - NATO STANAG 4347
[3] - Родионов С.А. Основы оптики. Конспект лекций. - СПБ: СПБ:  ГИТМО (ТУ), 2000. - 167 с.
[4] - Leno S. Pedrotti.  Basic Physical Optics. Open Access SPIE Publications.